Homotopy fiber
In mathematics, especially homotopy theory, the homotopy fiber is part of a construction that associates a fibration to an arbitrary continuous function of topological spaces 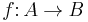 .
.
In particular, given such a map, define 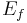 to be the set of pairs
to be the set of pairs 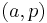 where
where 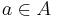 and
and ![p \colon [0,1] \to B](/2012-wikipedia_en_all_nopic_01_2012/I/34099a337e4bdb2a890f16b87214c079.png) is a path such that
is a path such that  . We give
. We give 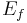 a topology by giving it the subspace topology as a subset of
a topology by giving it the subspace topology as a subset of 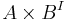 (where
(where 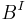 is the space of paths in
is the space of paths in  which as a function space has the compact-open topology). Then the map
which as a function space has the compact-open topology). Then the map 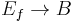 given by
given by 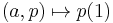 is a fibration. Furthermore,
is a fibration. Furthermore, 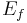 is homotopy equivalent to
is homotopy equivalent to  as follows: Embed
as follows: Embed  as a subspace of
as a subspace of 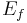 by
by 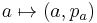 where
where 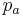 is the constant path at
is the constant path at 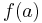 . Then
. Then 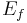 deformation retracts to this subspace by contracting the paths.
deformation retracts to this subspace by contracting the paths.
The fiber of this fibration (which is only well-defined up to homotopy equivalence) is the homotopy fiber 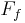 , which can be defined as the set of all
, which can be defined as the set of all 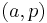 with
with 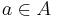 and
and ![p \colon [0,1] \to B](/2012-wikipedia_en_all_nopic_01_2012/I/34099a337e4bdb2a890f16b87214c079.png) a path such that
a path such that  and
and 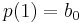 , where
, where 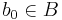 is some fixed basepoint of
is some fixed basepoint of  .
.
References
- Hatcher, Allen (2002), Algebraic Topology, Cambridge: Cambridge University Press, ISBN 0-521-79540-0, http://www.math.cornell.edu/~hatcher/AT/ATpage.html.